Electromagnetic (EM) methods measure time varying electric and magnetic fields to understand the subsurface.
Induction¶
Physically time varying electric and magnetic fields are connected through induction which is governed by the right-hand-rule. With your right hand, if you have an electric field propagating in the direction of your thumb a magnetic field will be induced in the direction of your fingers, notice the angle between is 90 degrees or orthogonal. Note the fields will also be 90 degrees out of phase, so that when one has a peak the other other is at a zero which obeys the laws of energy conservation, of course these principles are for electromagnetic waves travelling in free space, in a material propagation is much more complicated.
Diffusion¶
Most geophysical EM methods measure frequencies that are low enough such that a material’s dielectric properties are negligable, meaning that energy is not stored in the material it is only lost. The consequence of this is that EM fields no longer propagate through a material as waves, they propagate through a material diffusively. This means that the fundamental equations to represent EM propagation in the subsurface are different then the more common seismic methods. Instead of the wave equation, EM methods use the diffusion equation, which is the same as the wave equation minus the storage term. The exception is ground-penetrating radar (GPR). GPR measures frequencies high enough to intiate rotation of atomic dipoles making the dielectric permittivity measureable such that EM energy can be stored, thus allowing for wave propagation like seismic methods.
The main physical side effect of diffusion is that energy is only lost to the system, there are no reflections or refractions of the EM waves. However, because we are dealing with electromagnetics a magnetic field will induce an electric field and vice-versa. Furthermore, induction between the two fields is a linear process where the Earth acts as a linear filter controlling how one field transforms into the other and is dictated by properties of the subsurface, in particular electrical resistivity. Therefore, if we measure a source field and measure the secondary induced field we can deduce physical properties of the subsurface by calculating the transfer function between the primary and secondary fields.
Depth of Penetration¶
The depth to which EM fields will penetrate the subsurface is dependent on the source field frequency () and subsurface electrical resistivity (). This is called the skin depth (δ), the depth to which an EM field has decayed to a factor of .
Some rules of thumb:
- High frequencies, or short periods, will penetrate shallow whereas low frequencies long periods, will penetrate deeper. An analogy for this process is sound. High pitches are only heard nearby, whereas deep bass can be heard at large distances.
- Low resistivity, high conductivity, will absorb EM energy because these materials allow ions to flow easily. The easier it is for ions to move then the more energy it will soak up. Conversely, high resistivity, low conductivity, will allow energy to pass through easier because ions are more difficult to move.
Electrical Resistivity¶
Electrical resistivity is a physical property of a material that describes how well an electrical current can flow through the materal. Materials that are electrically conductive have interconnected ions like metals or fluids in an interconnected pore space. In the subsurface, electrical resistivity is sensitive to where fluids are or have been. Most mineral systems were emplaced by some type of magmatic or hydrothermal fluid along existing pathways, these often show up as electrical conductors in the data. In active systems or shallower in the crust where fluids are free to move around, the electrical resistivity will be low. Common settings are sedimentary basins. Salinity is the main driver of electrical resistivity of fluids, and temperature has a minor effect.
Electrical resistivity of subsurface materials can vary by orders of magnitude. A graphite body or salt water zone could be less than 1 where as a cratonic body may be greater than 10E4 . The main driver again is fluid content, or pore space content and connectivity of conductive phases.
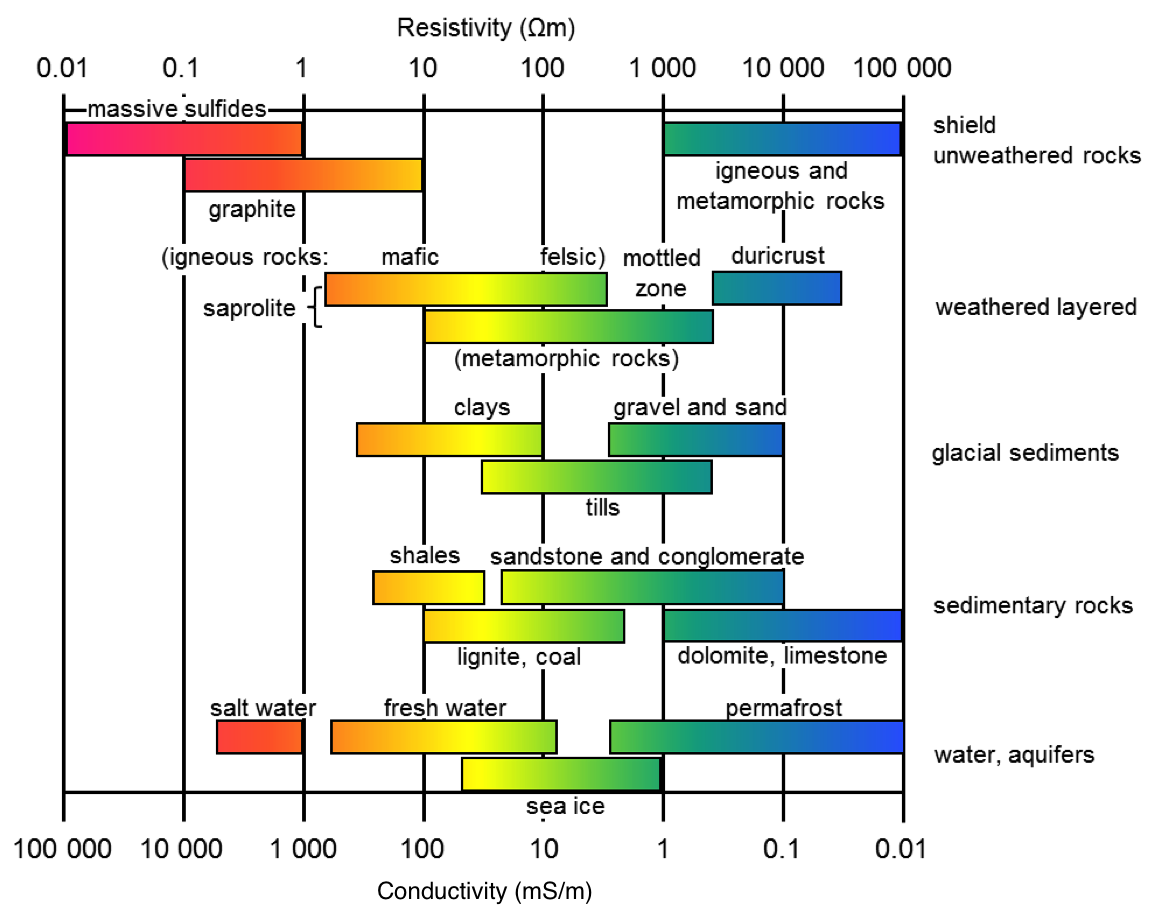
Figure 1:General electrical resistivity of geologic materials. Notice the span of values over orders of magnitude. Also, many materials have similar resistivity ranges enforcing the need for additional information to interpret resistivity models.
More Information¶
Click on the link for a thorough introduction to electromagnetic geophysics.